
一、单循环链表
1.回顾单链表
单链表,由于每个结点只存储了向后的指针,到了尾部标识就停止了向后链的操作。也就是说,按照这样的方式,只能索引后继结点不能索引前驱结点。
单链表的问题:如果不从头结点出发,就无法访问全部结点
解决方法:只需要将单链表中的终端结点的指针由空指针改为指向头结点
2.单循环链表
将单链表的终端结点的指针由原来的空指针改为指向头结点,就是整个单链表形成一个环,这种头尾相接的单链表称为单循环链表,简称循环链表,如下图所示。 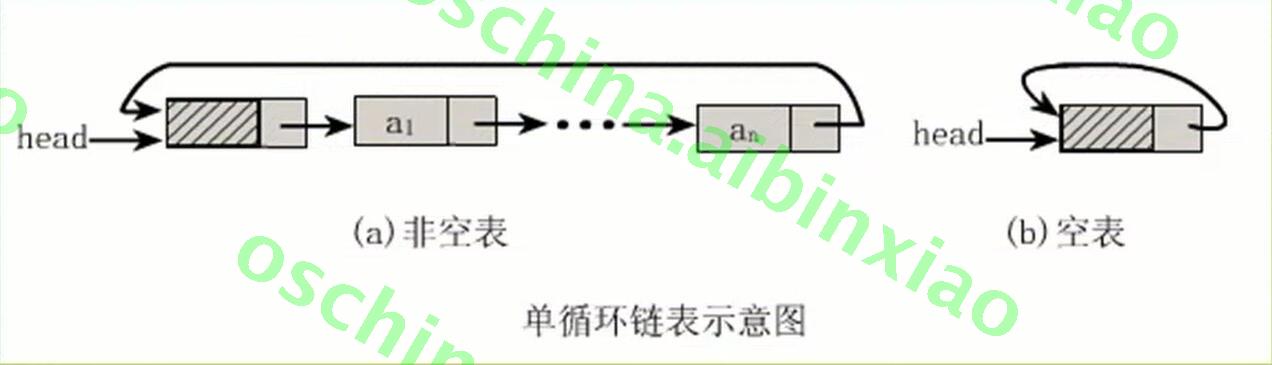
注意:
- 这里并不是说循环链表一定要有头结点;
- 其实循环链表的单链表的主要差异就在于循环的判断空链表的条件上,原来判断head->next是否为NULL,现在则是head->next是否等于head;
- 由于终端结点用尾指针rear指示,则查找终端结点是O(1),而开始结点是rear->next->next,当然也是O(1)。
3.初始化单循环链表的代码实现
// 初始化循环链表void ds_init(node **pNode){ int item; node *temp; node *target; printf("输入结点的值,输入0完成初始化\n"); while(1){ scanf("%d", &item); fflush(stdin); // 清除缓冲区 if(item == 0) return; if((*pNode) == NULL){ // 循环链表中只有一个结点 *pNode = (node*)malloc(sizeof(struct CLinkList)); if(!(*pNode)){ exit(0); } (*pNode)->data = item; (*pNOde)->next = *pNode; }else{ //找到next指向的第一个结点的结点 for(target = (*pNode);target->next != (*pNode);target = target->next); // 生成一个新的结点 temp = (node *)malloc(sizeof(struct CLinkList)); if(!temp){ exit(0); } temp->data = item; temp->next = *pNode; target->next = temp; } }} 4.循环链表插入结点的代码实现
// 插入结点// 参数:链表的第一个结点,插入的位置void ds_insert(node **pNode, int i){ node *temp; node *target; node *p; int item; int j = 1; printf("输入要插入结点的值:"); scanf("%d", &item); if(i == 1){ // 新插入的结点作为第一个结点 temp = (node *)malloc(sizeof(struct CLinkList)); if(!item){ exit(0); } temp->data = item; // 寻找到最后一个结点 for(target = (*pNode); target->next != (*pNode); target = target->next); temp->next = (*pNode); target->next = temp; *pNode = temp; }else{ target = *pNode; for( ; j<(i-1); ++j){ target = target->next; } // target指向第三个元素的 temp = (node *)malloc(sizeof(struct CLinkList)); if(!temp){ exit(0); } temp->data = item; p = target->next; target->next = temp; temp->next = p; }} 5.单循环链表删除结点的代码实现
// 删除结点void ds_delete(node **pNode, int i){ node *target; node *temp; int j = 1; if(i == 1){ //删除的是第一个结点 //找到最后一个结点 for(target = *pNode; target->next != *pNode; target = target->next); temp = *pNode; // 要删除的结点 *pNode = (*pNode)->next; // 记录待删除结点的下一个结点 target->next = *pNode; // 将最后一个结点的指针指向待删除结点的下一个结点 free(temp); }else{ target = *pNode; for( ; j next; } temp = target->next; // 要删除的结点 target->next = temp->next; free(temp); }} 6.单循环链表返回结点所在位置的代码实现
// 返回结点所在位置int ds_search(node *pNode, int elem){ node *target; int i = 1; for(target = pNode; target->data != elem && target->next != pNode; ++i){ target = target->next; } if(target->next == pNode)// 表中不存在该元素 return 0; else return i; } 7.单循环链表的特点
- 回顾单链表,我们有了头结点时,我们可以用O(1)的时间访问第一个结点,但对于要访问最后一个结点,我们必须要挨个向下索引,所以需要O(n)的时间。
- 然而,我们学习到循环链表的特点后,只需要用O(1)的时间就可以由链表指针访问到最后一个结点。
- 不过,我们需要改造一下现有的循环链表,我们不用头指针,而是用指向终端结点的尾指针来表示循环链表,此时查找开始结点和终端结点都很方便了,如图:

那么这个改造后的循环链表判断是否为空链表的条件就是:rear 是否等于 rear->next
循环链表的特点:无须增加存储量,仅对链接方法稍作改变,即可使得表处理更加方便灵活。
8.一个关于使用改造后单循环链表的题目
实现将两个线性表(a1,a2,...,an)和(b1,b2,...,bm)连接成一个线性表(a1,...,an,b1,...,bm)的运算?
分析:
- 若在单链表或头指针表示的单循环链表上做这种链接操作,都需要遍历第一个链表,找到结点an,然后将结点b1链到an的后面,其执行时间是O(n);
- 若在尾指针表示的单循环链表上实现,则只需要修改指针,无须遍历,其执行时间是O(1)。
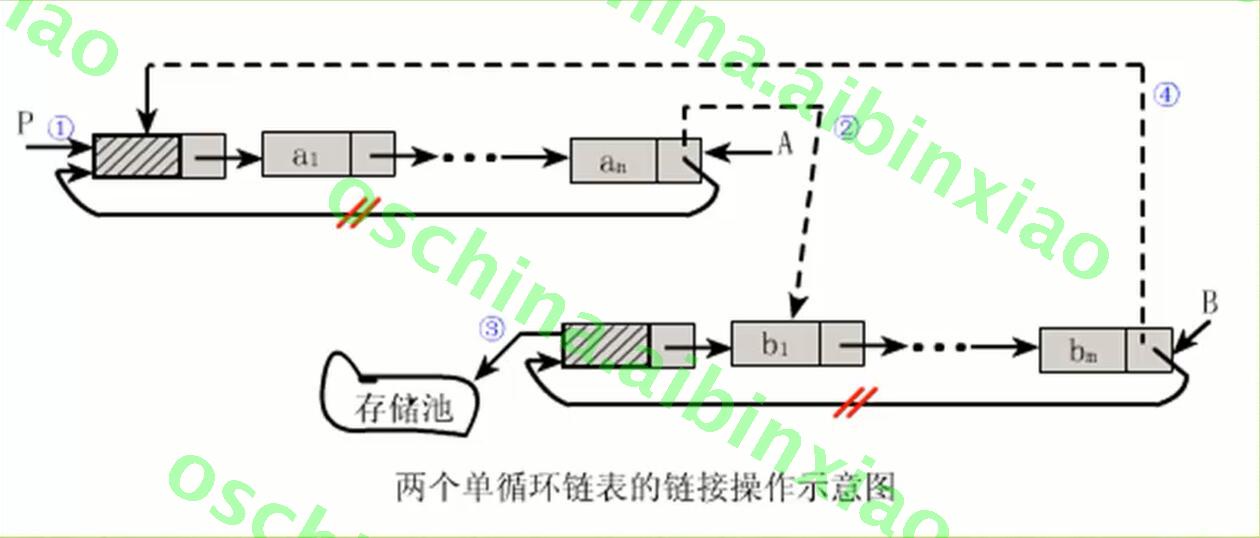
具体实现步骤分析:
- 1,把单循环链表A的rear不再指向头结点;
- 2,把单循环链表A的rear指向单循环链表的b1;
- 3,将单循环链表B的头结点释放掉;
- 4,将单循环链表B的rear指向原来单循环链表A的头结点。
代码实现:
// 假设A,B均为非空循环链表的尾指针LinkList Connect(LinkList A, LinkList B){ LinkList p = A->next; // 保存A表的头结点位置 A->next = B->next->next; // B表的开始结点链接到A表的尾部 free(B->next); // 释放B表的头结点 B->next = p; // B表的rear指向A表的头结点 return B;} 9.判断单链表中是否有环
有环的定义:链表的尾结点指向了链表中的某个结点,如图:
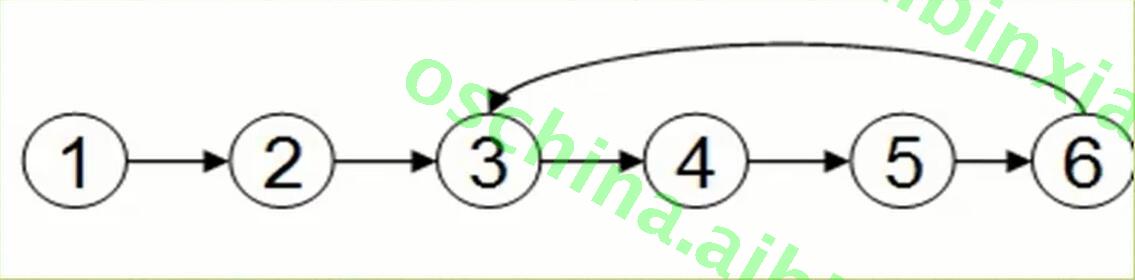
判断单链表是否有环,主要有两种方式:
- 方法一,使用p,q两个指针,p总是向前走,但是q每次都从头开始走,对于每个结点,看p走的步数是否和q一样。如图,当p从6走到3时,用了6步,此时若q从head出发,则只需两步就到3,因而步数不等,出现矛盾,存在环。
- 方法二,使用p,q两个指针,p每次向前走一步,q每次向前走两步,若在某个时候p == q,则存在环。
代码实现:
// loop.c#include "studio.h"#define OK 1#define ERROR 0#define TRUE 1#define FALSE 0typedef int Status; // Status是函数的类型,其值是函数结果的状态代码,如OK等typedef int ElemType; // ElemType类型根据实际情况而定,这里假设为inttypedef struct Node{ ElemType data; struct Node *next;}Node, *LinkList;// 初始化带头结点的空链表Status InitList(LinkList *L){ *L = (LinkList)malloc(sizeof(Node)); // 产生头结点,并使L指向此头结点 if(!(*L)){ // 存储分配失败 return ERROR; } (*L)->next = NULL; // 指针域为空 return OK; }// 初始条件:顺序线性表L已存在,操作结果:返回L中数据元素个数int ListLength(LinkList L){ int i =0; LinkList p = L->next; // p指向第一个结点 while(p){ i++; p = p->next; } return i;}// 随机产生n个元素的值,建立带表头结点的单链线性表L(头插法)void CreateListHead(LinkList *L, int n){ LinkList p; int i; srand(time(0)); // 初始化随机数种子 *L = (LinkList)malloc(sizeof(Node)); (*L)->next = NULL; // 建立一个带头结点的单链表 for(i=0; i data = rand()%100 + 1; // 随机生成100以内的数字 p->next = (*L)->next; (*L)->next = p; // 插入到表头 } }// 随机产生n个元素的值,建立带表头结点的单恋线性表L(尾插法)void CreateListTail(LinkList *L, int n){ LinkList p, r; int i; srand(time(0)); // 初始化随机数种子 *L = (LinkList)malloc(sizeof(Node)); // L为整个线性表 r = *L; // r为指向尾部的结点 for(i=0; i data = rand%100 + 1; // 随机生成100以内的数字 r->next = p; // 将表尾终端结点的指针指向新结点 r = p; // 将当前的新结点定义为表尾终端结点 } r->next = (*L)->next->next; }// 比较步数的方法int HashLoop1(LinkList L){ LinkList cur1 = L; // 定义结点 cur1 int pos1 = 0; // cur1的步数 while(cur1){ // cur1结点存在 LinkList cur2 = L; // 定义结点cur2 int pos2 = 0; // cur2的步数 while(cur2){ // cur2结点不为空 if(cur1 == cur1){ if(pos1 = pos2){ //走过的步数一样 break; // 说明没有环 }else{ printf("环的位置在第%d个结点处。\n\n", pos2); return 1; } } cur2 = cur2->next; // 如果没有发现环,继续下一个结点 pos2++; // cur2的步数自增 } cur1 = cur1->next; // cur1继续向后一个结点 pos1++; // cur1的步数自增 } return 0;}// 利用快慢指针的方法int HasLoop2(LinkList L){ int step1 = 1; int step2 = 2; LinkList p = L; LinkList q = L; while(p!=NULL && q!=NULL && q->next!=NULL){ p = p->next; if(q->next != NULL){ q = q->next->next; printf("p:%d, q:%d \n", p->data, q->data); } if(p == q){ return 1; } } return 0; }int main(){ LinkList L; Status i; cahr opp; ElemType e; int find; int tmp; i = InitList(&L); printf("初始化L后:LinkLength(L)=%d\n", ListLength(L)); printf("\n1.创建有环链表(尾插法) \n2.创建无环链表(头插法) \n3.判断链表是否有环 \n0.退出 \n\r"); while(opp != '0'){ scanf("%c", &opp); switch(opp){ case '1': CreateListTail(&L, 20); printf("成功创建有环L(尾插法)\n"); printf("\n"); break; case '2': CreateListHeadl(&L, 20); printf("成功创建无环L(头插法)\n"); printf("\n"); break; case '3': printf("方法一:\n\n"); if(HasLoop1(L)){ printf("结论:链表有环\n\n\n"); }else{ printf("结论:链表无环\n\n\n"); } printf("方法二:\n\n"); if(HasLoop2(L)){ printf("结论:链表有环\n\n\n"); }else{ printf("结论:链表无环\n\n\n"); } printf("\n"); break; case '0': exit(0); } } }
本文为原创文章,如果对你有一点点的帮助,别忘了点赞哦!比心!如需转载,请注明出处,谢谢!